FSI in PreonLab - Sloshing Tank with Elastic Beam

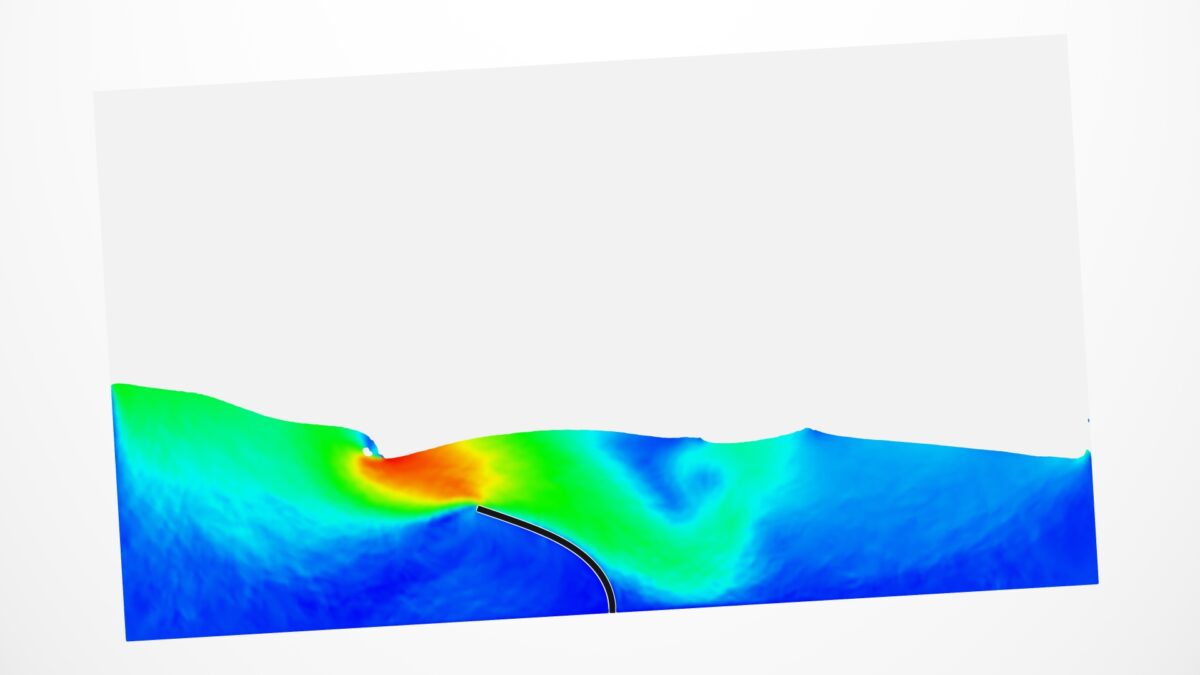
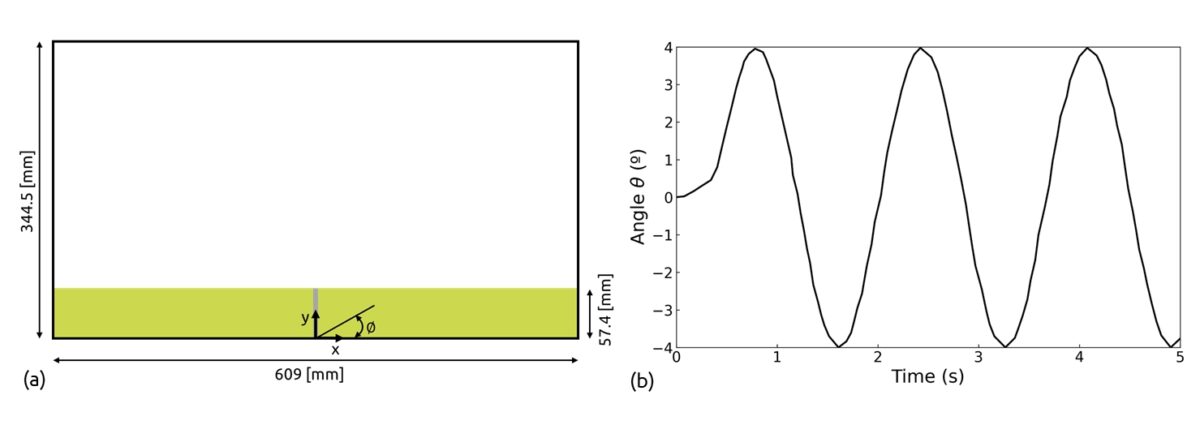
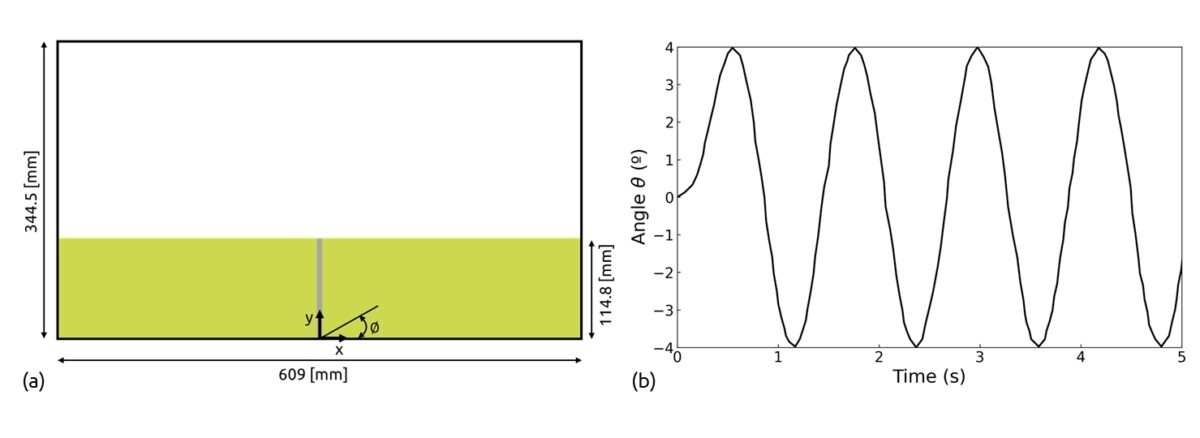
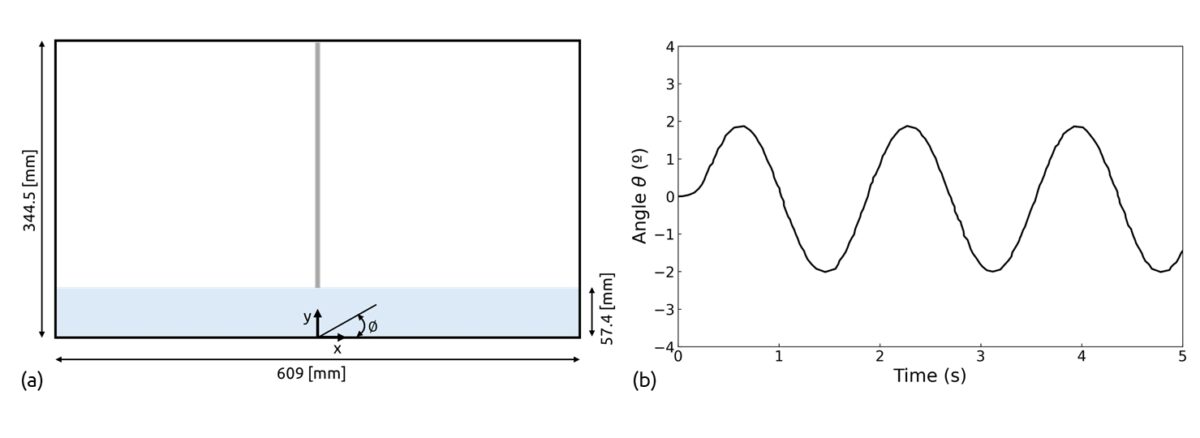
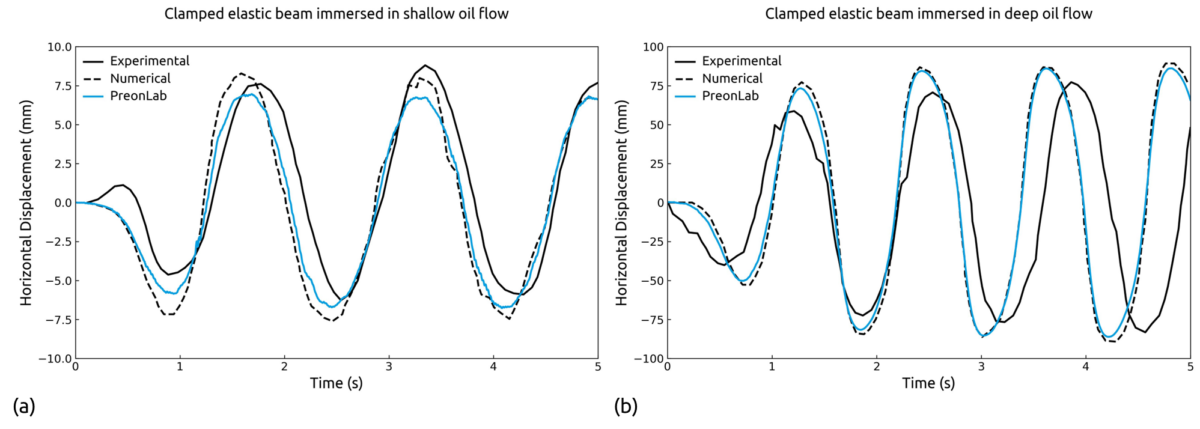
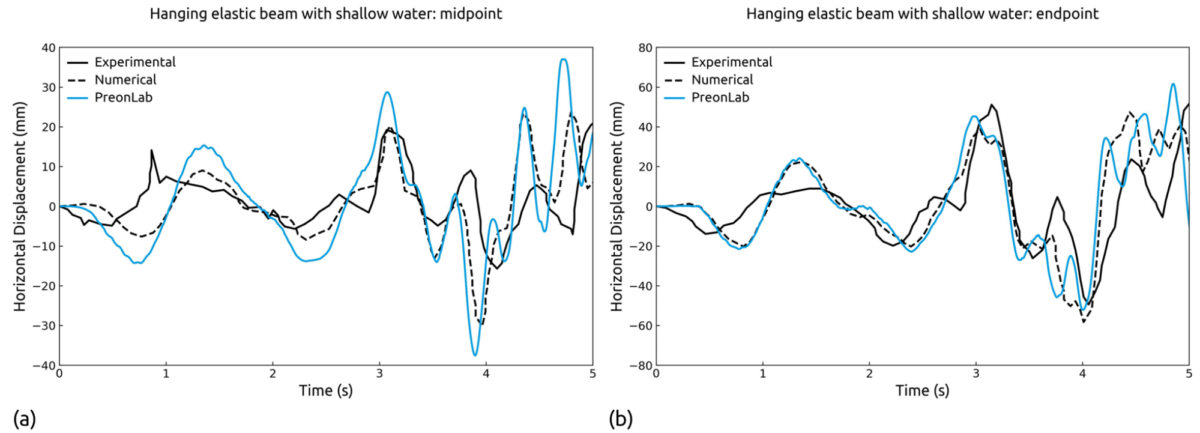
FSI involves the interaction between fluid and solid domains, where the motion and forces in one domain influence the other, and vice versa. In many real-world scenarios, fluid flows interact with deformable solid bodies. While the deformation of these solid bodies is typically minimal and can be neglected in most simulations, there are cases where this interaction becomes significant. For instance, in a soiling simulation, the deformation of components like mudflaps can influence the behavior of the fluid. Another case is the movement of windshield wipers interacting with rainwater. In this scenario, the deformation of the wiper blades plays a significant role and can influence simulation results. Figure 1 shows the velocity field in a sloshing tank with a flexible beam simulation, where such fluid and solid interaction is considered. The simulation has been performed in PreonLab 6.2.

Smoothed Particle Hydrodynamics (SPH) has become one of the most popular methods for modeling free-surface flows. With its Lagrangian formulation and mesh-free method, SPH has an advantage over other computational methods in solving simulations with large fluid deformations, complex geometries, and dynamic interfaces. The inherent advantages of the SPH method, coupled with a strong focus on usability, make PreonLab a powerful, reliable and user-friendly simulation tool.

With the introduction of the linear elastic solver, PreonLab leverages the potential of the SPH method and the Lagrangian formulation to build a more capable tool in terms of multiphysics. However, the implementation of a linear elastic solver is not straightforward and presents several challenges. For instance, as SPH is naturally suited to problems involving large strains and deformations, it often requires enhanced formulations or specialized kernel functions to ensure accuracy in small deformation problems. Additionally, modeling rotation poses its own set of challenges, as discussed by Peer et al. [2]. Despite these challenges, the SPH-based FSI implementation in PreonLab offers notable advantages. One of the key benefits is its mesh-free interface handling, which eliminates the need for mesh element alignment at the fluid-solid interface, unlike traditional methods. This flexibility is especially valuable for simulating large deformations and highly dynamic interfaces.

In PreonLab 6.2, FSI problems are solved as a combined system, meaning that the fluid and elastic subproblems are solved within a single framework. This allows for more accurate and stable interaction between the two phases, as it avoids potential issues related to partitioned solvers that treat the fluid and solid phases separately. PreonLab 6.2 introduces a solver capable of modeling linear elastic solids on their own, or in a coupled multiphysics FSI context.

We have selected the benchmark of a sloshing tank with a deformable beam for the validation of the deformable solver as it provides a setup featuring free surface flow with a highly dynamic free surface, as well as significant deformations of the beam itself. Idelsohn et al. [1] presents three setups, which are analyzed using the Particle Finite Element Method and validated through experiments.

These are:

• Clamped elastic beam immersed in a shallow oil flow
• Clamped elastic beam immersed in deep oil flow
• Hanging elastic beam with shallow water

The setup of the first study case is described in Figure 2 (a). The tank used in the experimental validations by Idelsohn et al. [1] is made of methacrylate, with a length of 609.0 mm, a height of 344.5 mm, and a width of 39.0 mm.

The setup consists of a structure that supports a tank and an electrical engine, which generates a harmonic rolling motion on the moving part of the structure that surrounds the tank filled with liquid. It includes a high-precision torque meter with a 200 N·m range, commonly used in the design of passive anti-roll tanks for fishing vessels. The container was designed to move in an oscillatory motion around a fixed point, which in this study is located at the center of the tank’s bottom. Both the maximum angle and angular speed can be adjusted to match the critical sloshing frequencies for various liquid levels. Figure 2 (b) shows the angular motion of the tank over time, for the case with shallow oil. The container’s upper wall is sealed, but two holes are present at the top to allow air circulation without disrupting the behavior of the liquid.

In the setup of shallow oil flow, Figure 2a, the initial height of the oil is 57.4 mm. The density and dynamic viscosity of this commercial oil were measured and came to 917 kg/m³ and 4.585×10^-1 Pa·s, respectively. The beam attached to the bottom of the tank has a thickness of 4 mm and a width of 33.2 mm, making it effectively behave as a 2D beam, as it does not make contact with the tank walls during the sloshing motion. The minimum allowable gap is 2.9 mm. The elastic beam is made from a dielectric polyurethane resin branded as AXSON RE 11820-(9). The test samples have a density of 1100 kg/m³, and the Young modulus, determined through a tensile test, is approximately 6 MPa. Figure 3a shows the setup of the deep oil flow case. The difference between this and the first setup lies in the initial height of the oil phase and the length of the beam, both of which are 114.8 mm for the deep oil flow setup. The motion of the tank is also altered (Figure 3b).

The third setup introduces a few modifications compared to the previous two. The design of the setup is shown in Figure 4a. In this case, the working fluid is water, with an initial fluid height of 57.4 mm. Unlike the previous setups, the beam is attached to the top of the container. This beam has a length of 287.1 mm, with mechanical properties of 1900 kg/m³ for density and 4 MPa for the Young Modulus. In this way, the beam is denser and less rigid than the ones described above. Additionally, the tank’s tilt motion is restricted to a range between -2 and 2 degrees, as illustrated in Figure 4b.

Figure 5 shows the recorded frames of the sloshing tank motion for the shallow oil setup, including experimental, numerical, and PreonLab results. Similarly, Figure 6 presents the corresponding results for the deep oil flow setup.

In Figure 5, a close qualitative match can be observed between the PreonLab and the experimental/numerical results from the research paper. The free surface and the beam bending behavior are closely aligned across all the studied cases, indicating good agreement between the different methods

In the deep oil flow setup shown in Figure 6, the frames exhibit some differences compared to the previous ones. At 2.32 and 2.56 seconds, the free surface appears slightly different, and the beam in the PreonLab results appears to be bent more than in the experimental and numerical cases. Although these differences are not substantial, they represent a greater deviation compared to the results observed in the shallow oil flow setup.

Additionally, the horizontal displacement is tracked at the end point of the beam for the setups with shallow and deep oil. Figure 7 represents the horizontal displacement results for the clamp beam in shallow and deep oil.

The PreonLab results closely align with the trend and values, especially in comparison to the numerical results. For the deep oil case (Figure 7b), the fit is nearly perfect, whereas small quantitative deviations are observed in the shallow oil case (Figure 7a). Notably, a phase shift between the numerical and experimental results can be observed, particularly in Figure 7b. This discrepancy may be attributed to potential inaccuracies in the experiment, such as issues with the oscillator’s motion or measurement errors. As suggested in the reference paper, another potential cause of this phase shift could be the interaction between the side walls of the tank and the beam [1]. Although a gap of 2.9 mm was intentionally left in the experiment, the relatively slow fluid movement near the walls could influence the motion of the beam. This interaction introduces additional forces that can distort the beam’s motion, thereby contributing to the observed phase shift. Moreover, such interactions might cause small variations in the beam’s oscillatory behavior, which could explain the discrepancies between the numerical and experimental results.

The observation aligns with the increase in depth of the oil flow. The larger span of the beam in case of the deep oil flow setup results in a larger area affected by the beam-wall interactions. This effect could be the cause of the larger deviations between numerical and experimental beam deflections for higher tank filling ratios.

Figure 8 displays the recorded frames for the hanging elastic beam with shallow water setup.

In Figure 8, the results show a close similarity for times 2.96 s and 3.32 s. At 3.4 s, the free surface in PreonLab resembles more closely the numerical results than the experimental ones. Additionally, the beam bending is more pronounced in the PreonLab results. At 3.56 s, the free surface in PreonLab again aligns more with the numerical results, although the wave appears slightly more pronounced on the left side in PreonLab. Overall, the results remain fairly consistent across all methods. Figure 9 represents the horizontal displacement tracked for the hanging beam with shallow water setup. Figures 8a and 8b show the displacement measured at the midpoint and tip of the beam.

Once again, PreonLab demonstrates a trend that closely matches the numerical results for the horizontal displacement. In terms of the endpoint, as shown in Figure 9b, the values are in closer agreement.  Interestingly, both PreonLab and numerical results differ more from the experimental results when looking at the midpoint of the beam. As the beam tip is more in contact with the fluid, its motion will be mainly fluid-driven, while the midpoint is highly dynamic and driven by the elastic response. Here, the natural frequencies of the beam play an important role. Additionally, there might be differences in the natural frequencies of the beam from the experimental (3D) and numerical setup (2D), which can also justify the mismatch.

In this case, with water, since the beam is hanging from the top of the tank and is not in direct contact with the fluid, the interaction between the beam and the surrounding fluid is less than that in the other cases presented. Unlike the oil setup, where the fluid between the beam and side walls has a strong influence on the beam’s motion, only a small portion of the hanging beam is influenced by this effect. As a result, even though the motion is more chaotic, the phase shift might not be so apparent in this case.

The validation of the deformable solver using the sloshing tank benchmark has proven to be successful, with PreonLab delivering results that closely match both the numerical and experimental data across the various setups. In the case of the clamped elastic beam immersed in shallow and deep oil flows, PreonLab demonstrates a strong agreement with the numerical results, particularly for the deep oil case where the fit is nearly perfect. For the hanging elastic beam with shallow water, PreonLab again shows an excellent match with the numerical data, particularly in the endpoint displacement. Overall, this study shows PreonLab 6.2’s capabilities to handle complex FSI and highlights the potential of the new linear elastic solver.

[1] – Idelsohn, S. R., Marti, J., Souto-Iglesias, A., & Oñate, E. (2008). Interaction between an elastic structure and free-surface flows: Experimental versus numerical comparisons using the PFEM. Computers & Structures, 86(7–8), 659–674. https://doi.org/10.1016/j.compstruc.2007.01.030

[2] – Peer, A., Gissler, C., Band, S., & Teschner, M. (2017). An implicit SPH formulation for incompressible linearly elastic solids. Computer Graphics Forum, 36(7), 143-154. https://doi.org/10.1111/cgf.13317